Todo lo relacionado al modelismo en venezuela

El Centro de Gravedad es un punto critico que deberemos acondicionar para obtener las caracteristicas de vuelo de nuestro modelo. Ante un modelo terminado el aeromodelista se enfrenta a la pregunta del millon: Donde esta el Centro de Gravedad? .
La respuesta variara segun el modelo, y si su centro de gravedad va adelantado o retrasado respecto de este punto.-

Ubicando el Centro de Gravedad:

Cuando comenzamos a construir un modelo vemos que en los planos se ubica mediante un simbolo caracteristico el Centro de Gravedad. Tiene tres representaciones, pero la mas usada es la del ciculo dividido en cuatro, con 2 porciones blancas y las restantes dos de color negro.

Como vimos en la seccion Centrado de Modelos sujetando, con los dedos, nuestro modelo por la parte inferior del ala,(es decir el intrados),a la altura del centro de gravedad, se vera que el modelo adopta un cierto "equilibrio", en el caso de los modelos radiocontrolados esto se hace con todo el equipo de radio y motor ya instalados y el depósito de combustible vacío. Debemos saber, que el C.G. (Centro de Gravedad) lo condiciona el tipo usado de perfil y la forma alar de esta.

Si bien no hay un punto exacto del centro de gravedad, si hay ciertos limites dentro del cual se debe ubicar, fuera de ese margen no habra en el modelo un vuelo estable. Dentro de los limites mencionados, un centro de gravedad ADELANTADO resultara en un vuelo pesado de nariz, en el modelo. En cambio un Centro de Gravedad ATRASADO dara más maniobrabilidad, ideal para vuelo acrobático.-

Como calcular el C.G.:

Para calcular el C.G. deberemos tomar en cuenta la forma del ala y su perfil , en el caso de un:

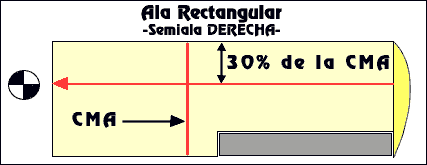
ALA RECTANGULAR: la mas comun, vemos como la cuerda es la misma desde la raíz al borde marginal, así que deberemos medir el 30 % ( en el caso de un perfil plano convexo). Una vez localizado el punto se hace desde él una perpendicular al eje longitudinal del avión y ahí estará localizado el centro de gravedad.-

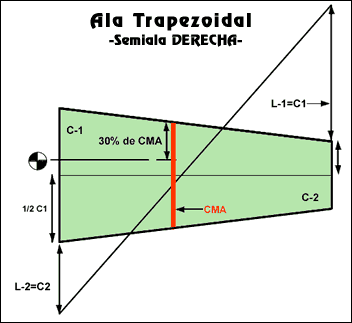
ALA TRAPEZOIDAL: tendremos que encontrar la Cuerda Media (CM) o Cuerda Media Aerodinámica (CMA). En cuanto a la longitud sabemos de antemano que es la media aritmética de la cuerda en la raíz de ala C-1 y la del extremo C-2 pero tenemos que localizarla geométricamente. Para ello dibujamos a tamaño natural o a escala la planta alar y trazamos una línea que una los dos puntos medios o centros geométricos (cg) de las dos cuerdas extremas. Después prolongamos a partir del borde de fuga, por ejemplo, la cuerda C-1 de la raiz en un valor igual a C-2. Haremos lo mismo en el marginal donde añadimos a C-2 una longitud igual a C-1 . Unimos los dos extremos de esta prolongaciones con una línea que va a cortar a la que unía los dos cg y en esa intersección se halla la Cuerda Media o CM. Sobre ella medimos el % que corresponda al perfil y desde ahí trazamos una perpendicular al eje longitudinal del avión lo que nos dará la situación exacta del Centro de gravedad.

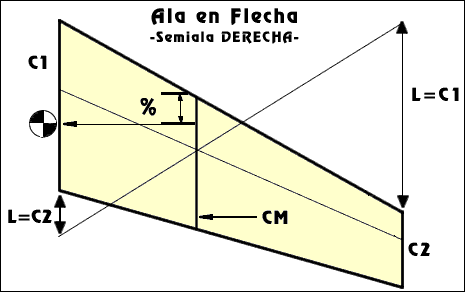
ALA EN FLECHA: Se calcula exactamente del mismo modo que en las trapezoidales. Lo único a destacar es lo retrasado que queda el centro de gravedad comparado con las rectangulares de ahí que los aviones con ala en flecha tengan la trompa tan corta

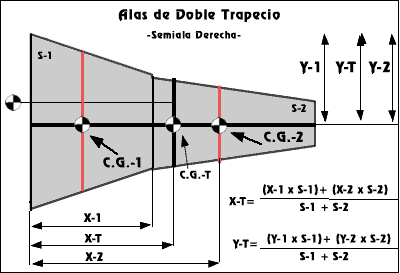
.ALAS EN DOBLE TRAPECIO: En este caso comenzamos por halla las CM de cada uno de los paneles (CM-1 y CM-2) lo que haremos como en el ejemplo del ala trapezoidal. Una vez conocidas las dos CM y localizados sus centros geométricos (CG1 y CG2) nos permitirá calcular las coordenadas (X e Y) del CG de la Cuerda Media de toda el ala (CM-T), poder dibujar ésta y colocar el centro de gravedad. Para ello usamos las siguientes fórmulas teniendo en cuenta que S-1 y S-2 son las superficies de cada uno de los paneles alares :

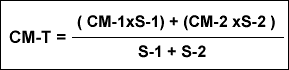
Con las fórmulas y el gráfico siguiente localizamos el centro geométrico total (CGT) a través del cálculo de sus coordenadas y podemos trazar la cuerda media total (CMT) como habíamos dicho antes. En el caso representado en el gráfico todos los valores de Y son iguales, pero en la mayoría de los casos no ocurrirá esto. Hay que recordar que el área de un trapecio es la semisuma de las bases X (por) la altura.-

EN LOS BIPLANOS: Nos podemos encontrar dos casos diferentes, que las dos alas tengan la misma superficie o que sean diferentes (sesquiplanos). En el primer caso, alas de idéntica cuerda y envergadura consideramos como si fuera un monoplano cuya CM sería la distancia entre el borde de ataque de la CM del ala más adelantada (suele ser la superior) y el borde de fuga de la CM del ala más retrasada. Teniendo esta cuerda medimos el % que corresponda, según perfil, y ya tenemos el centro de gravedad.

EN LOS BIPLANOS DE ALAS DESIGUALES: Se parte de calcular por separado la posición del centro de gravedad en cada una de las alas. La distancia que separa estos dos centros, en el plano horizontal, la llamamos "D" y a la superficie de cada ala S-1 y S-2 respectivamente. Hallando el valor "d" que es la distancia , horizontal, entre la posición del centro de gravedad del ala superior y la posición del centro de gravedad conjunto de ambas alas.

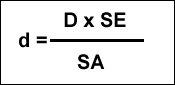
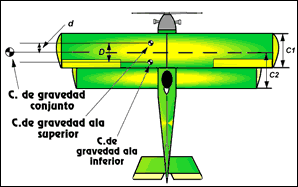
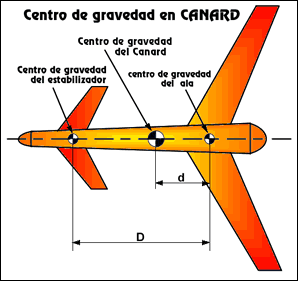
EN LOS MODELOS "CANARDS":: En este tipo de avión el estabilizador va por delante del ala y a efectos de sustentación hay que considerarlo como otra ala. Calcularemos la posición del teórico centro de gravedad del ala y del estabilizador así como sus respectivas superficies. Aplicando la fórmula abajo indicada donde D es la distancia entre los centros de gravedad de ala y estabilizador. "d" sería la distancia entre el c. de g. del ala y el C. de gravedad efectivo del avión. SA y SE son las superficies de ala y estabilizador.